|
АHТОHЮК П.Н. ЗОЛОТОЕ СЕЧЕHИЕ - МАТЕМАТИЧЕСКИЙ ТЕРМИH ЛЕОHАРДО ДА ВИHЧИ
Главная → Публикации → Материалы международной конференции → Антонюк П.Н. Золотое сечение - математический термин Леонардо да Винчи
"Пусть не читает меня в основаниях моих тот, кто не математик", - заявлял Леонардо да Винчи, перефразируя девиз Платоновской академии "Негеометр да не войдет!" Такими словами он выразил свое отношение к математике, интерес к которой во многом сформировался под влиянием его друга, итальянского математика Луки Пачоли. В конце XV в. Леонардо да Винчи ввел термин "золотое сечение", означающий такое деление отрезка на две части, когда большая его часть является средним геометрическим всего отрезка и меньшей его части. Часто под золотым сечением понимают иррациональное число τ = 1,6180339887498948482045868343656381177203091798... , равное отношению большей и меньшей частей отрезка.
Иррациональное число τ было известно намного раньше. Еще Евклид использовал золотое сечение при построении правильных 5- и 10-угольников, а также двух правильных многогранников Платона, додекаэдра и икосаэдра1. Золотое сечение широко применялось в геометрии и искусстве, в первую очередь в архитектуре. В 1509 г. в Венеции вышла книга Пачоли "О божественной пропорции", содержащая теорию геометрических пропорций 2. Пачоли указывает 13 свойств божественной пропорции (золотого сечения), чтобы почтить 12 апостолов и их учителя Иисуса Христа, и утверждает, что для перечисления всех свойств божественной пропорции не хватило бы чернил и бумаги. Леонардо да Винчи сделал рисунки для этого сочинения, в том числе 59 изображений многогранников.
Итальянский математик Леонардо Пизанский (Фибоначчи) издал в 1202 г. "Книгу абака" - трактат об арифметике и алгебре. В этой книге рассмотрена задача о разведении кроликов. Ежемесячное увеличение числа пар кроликов описывается последовательностью Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ... , в которой сумма соседних чисел равна последующему числу. Эта последовательность асимптотически ведет себя как геометрическая прогрессия со знаменателем, равным золотому сечению 3. О важной роли числа τ среди других чисел говорит то, что при разложении его в так называемую непрерывную или цепную) дробь получается бесконечная последовательность единиц. С додекаэдром и икосаэдром тесно связан открытый немецким астрономом и математиком Иоганном Кеплером правильный ромбический многогранник, триаконтаэдр 4. 30 граней многогранника - это ромбы, отношения диагоналей которых равны золотому сечению. Среди граней некоторых полуправильных многогранников Архимеда встречаются 5- и 10-угольники; следовательно, при их построении необходимо использовать золотое сечение 5. Появление золотого сечения при описании конфигураций многогранников и вообще геометрических тел объясняется наличием у этих тел осей симметрии пятого порядка: при повороте тела вокруг некоторой оси на угол, равный одной пятой части полного оборотадело совмещается само с собой. Интересно, что у бесконечно протяженных в трехмерном пространстве правильных дискретных систем, кристаллов, оси симметрии пятого порядка отсутствуют, хотя есть оси симметрии порядков 2, 3, 4 и 6. Это означает, что при описании симметрии кристаллов можно обойтись без золотого сечения. Наоборот, открытые в конце XX в. молекулярные кластеры и квазикристаллы могут иметь оси симметрии пятого порядка, а, следовательно, их структура может быть связана с золотым сечением 6. Давно замечено, что в строении некоторых растений и животных присутствуют оси симметрии пятого порядка. Яркими примерами такой симметрии могут служить цветок яблони и морской ёж. В отличие от кристаллов живой мир допускает геометрию золотого сечения. Золотое сечение часто встречается в разных областях естественно-научного знания. Например, скорость сходимости хорошо известного итерационного метода секущих, применяемого для поиска корней уравнений, равна золотому сечению. Существует несколько итерационных методов вычисления золотого сечения, входящих в число наиболее интересных математических задач. Мы попытались их определить и систематизировать. К числу принципиальных свойств методов нахождения золотого сечения относятся их простота и скорость вычисления (скорость сходимости), что и легло в основу предложенной систематизации. Вначале рассмотрим медленные методы вычисления τ. Так как золотое сечение 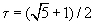 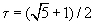 является положительным корнем уравнения х2= х+1, то вычисление τ методом последовательных приближений осуществляется по формулам 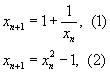 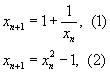 Для которых начальное приближение х0 выбирается произвольно. Последовательность (1) медленно сходится к τ. Последовательность (2) медленно расходится от τ, или, другими словами, медленно сходится к τ при п → -∞, поэтому в данном случае вычислять τ следует по обратной формуле 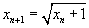 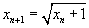 .
Важно отметить, что последовательность (1) при х0=1 тесно связана с числами Фибоначчи fn: 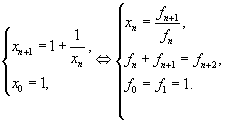 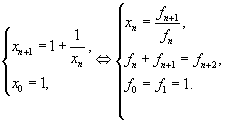 Таким образом, числа Фибоначчи образуют числители и знаменатели дробей в сходящейся к τ последовательности: 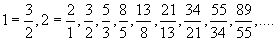 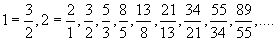 Данная последовательность распадается на две подпоследовательности нижних и верхних оценок для τ: 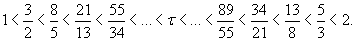 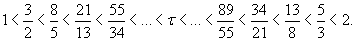 Рассмотрим теперь быстрые методы вычисления τ. Формула 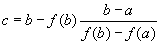 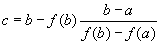 уточняет два приближения a и b к корню функции f(x). Формула 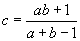 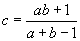 уточняет два приближения a и b к корню τ функции f(x)=x2-x-1.
В частном случае, когда а=хп-1, b=xn, c=xn+1, получаем для вычисления τ формулу метода секущих 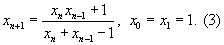 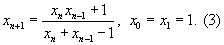 В частном случае, когда а=хп, b=xn, c=xn+1, получаем для вычисления τ формулу метода касательных 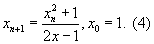 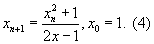 Начальные приближения x0 и х1,в формулах (3) и (4) можно выбирать произвольно.
Разностные уравнения (1), (2), (3), (4) можно записать и в другой форме – как итерации функций и отображений. Такая форма записи удобна в случае громоздких уравнений. Например, уравнение (4) соответствует итерациям функции 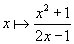 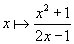 , а уравнение (3) соответствует итерациям отображения: 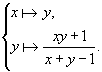 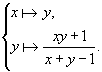 Используя нелинейное преобразование (так называемый корректор линейной сходимости или линейной расходимости) 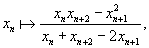 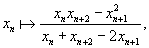 получаем возможность преобразовывать задаваемые формулами (1) и (2) функции 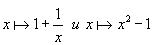 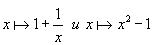 в новые функции: в новые функции: 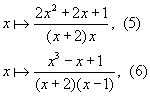 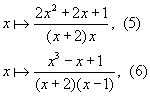 задающие быстро сходящиеся к τ итерации.
Используя так называемый корректор квадратичной сходимости 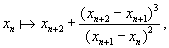 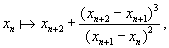 преобразуем задаваемую формулой (4) функцию 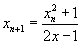 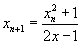 в новую функцию в новую функцию 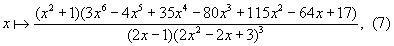 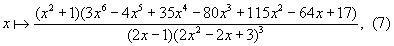 дающую сверхбыструю сходимость к τх. Каждая итерация функции (7) увеличивает число взятых после запятой правильных десятичных знаков приближенного значения τ более чем в 6 раз! Всего 9 итераций равного единице на чального приближения дают более трех миллионов десятичных знаков, а 13 итераций - более четырех миллиардов десятичных знаков.
Для полноты представления о методах нахождения золотого сечения необходимо разъяснить такое понятие, как "скорость сходимости". Если для последовательности xn, сходящейся к пределу х*, верна формула 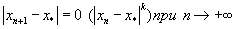 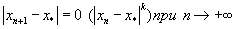 (k - положительное действительное число), то k называется скоростью сходимости данной последовательности. Для формулы (1) k=1 (линейная сходимость). Для формул (4), (5) и (6) k=2 (квадратичная сходимость). Для формулы (7) k=6. Формула (2) задает линейную расходимость. Наконец, в соответствии со сказанным выше формула (3), как вариант метода секущих, характеризуется скоростью k=τ: число τ вычисляется со скоростью τ.
Число τ входит в список важнейших математических постоянных, таких, как число π, число е, число γ (постоянная Эйлера-Маскерони) и т.д. Более 500 лет вслед за Леонардо да Винчи это число называют золотым сечением.
Примечание
|
|